Исследование рынков

Введение

Маркетинг относится в основном к сфере эмпирических исследований. Все что мы знаем о нем — либо опыт компаний, накопленный за десятилетия их работы на различных рынках, либо плоды исследований психологов, социологов, экономистов и других ученых. Предметом маркетинга, как научной дисциплины, является деятельность фирмы на рынке во всем ее беспредельном разнообразии. Отсюда сложность и неоднозначность рассуждений маркетологов, а также их скептицизм в отношении строгих математических выкладок которыми часто пользуются экономисты-теоретики или специалисты в области финансового анализа. Действительно, как переложить на язык чисел и формул, например, поведение сотен тысяч различных потребителей на рынке и учесть при этом идеи нескольких десятков специалистов, работающих в разных фирмах и стремящихся к различным целям?

И, тем не менее, в определенных ситуациях применение математических моделей для анализа маркетинговой деятельности фирмы или при исследовании рынков, не только возможно, но и может оказать существенную помощь разработчикам бизнес-планов компании, когда встанет вопрос об эффективности и рисковости инвестиций в тот или иной бизнес. Главное, чтобы в применяемых моделях производился надлежащий учет неопределенности относительно будущего состояния учтенных в модели параметров рынка.

В работах по маркетинговому моделированию (например, [1]) упомянутая неопределенность учитывается с введением в модель так называемых субъективных вероятностей, оценки которых получены как результат познавательной активности экспертов или экспертных групп. Подробнее о применимости вероятностных методов в экономичееских задачах см. [2]. Мы не хотели бы сейчас занимать внимание читателя дискуссионными вопросами о том, насколько вообще корректно и удобно применение вероятностей в экономическом анализе (в [2] этому посвящен отдельный раздел). Скажем лишь, что для нас сегодня более предпочтительным способом учета неопределенности является подход, основанный на математике нечетких множеств, заложенной 35 лет назад американским ученым Л.Заде.

Целью настоящей работы как раз и является раскрытие возможностей нечетко-множественного подхода в маркетинговом анализе, что будет подтверждено результатами расчетного примера.

Но сначала затронем общие вопросы теории маркетингового моделирования.

Построение маркетинговой модели

Любая модель является сильно упрощенным отражением действительности. Важно, чтобы это упрощение не сделало рассуждения исследователя тавтологичными. Этого следует избегать, тщательно описывая допущения (условия применимости) модели. Если допущения модели противоречат специфике объекта исследования (рынка того или иного товара), то модель используется некорректно.

В качестве примера приведем комплекс возможных допущений модели продаж на так называемом ограниченном рынке:

• Период наблюдения ограничивается временем с момента появления товара (торговой марки) на рынке до момента достижения фирмой максимальной доли рынка.
  
  Замечание. Определение максимальной доли рынка — сложная задача, связанная с многофакторным анализом рыночных структур. Ее решение было бы неуместно в рамках настощей работы. Поэтому параметр максимальной доли рынка можно в рамках данной модели мы заменим параметром целевой доли рынка. Количественные цели, связанные с увеличением объема продаж или рыночной доли ставят устанавливаются в большинстве фирм.
• Емкость рынка (то есть совокупный объем продаж на рынке за период) является постоянной величиной или прирастает, за счет равномерного увеличения объемов продаж всех поставщиков.
  
  Замечание. В реальности емкость рынка может изменяться с течением времени под воздействием различных факторов: изменение числа потребителей (например, изменение численности населения или подключение новых групп людей к числу потребителей данного продукта), изменение интенсивности потребления (например, в связи со сменой сезонов, или под воздействием рекламных мероприятий). При этом условие равномерности может не соблюдаться, а это значит, что абсолютная величина целевой рыночной доли фирмы в единицах проданного товара может изменяться под воздействием непредсказуемых внешних факторов.
• Число поставщиков на рынке является неизменным. Чтобы избежать усложнения модели, исследователи не берут во внимание возможное вторжение на рынок новых конкурентов или отказ имеющихся поставщиков от работы на нем.
• Маркетинговые усилия фирмы являются единственным эндогенным фактором, воздействующим на действительную величину ее рыночной доли.

Все параметры маркетинговой модели мы условно разбиваем на три класса: экзогенные, промежуточные и целевые. Класс экзогенных параметров образуют те параметры рынка, которые по допущениям рассматриваются как внешние по отношению к построенной модели (например, число потребителей на рынке или зависимость интенсиности потребления от маркетинговых усилий компаний). То есть в модели предполагается, что никакое количественное изменение параметров модели не повлияет на величину экзогенных параметров. Все прочие (эндогенные) параметры модели, наоборот, являются функционально зависимыми от уровня экзогенных параметров. Эти внутренние параметры мы условно разбиваем на промежуточные (используемые во внутримодельных расчетах и не имеющие самостоятельной ценности для исследователя) и целевые (которые непосредственно контролируются исследователем, и по состоянию которых исследователь делает те или иные выводы о состоянии рынка).

Мы предполагаем далее, что разработанная исследователем маркетинговая модель является функциональной, т.е. все связи между параметрами модели вполне четко формализованы и имеют функциональное описание. Это было бы не так, если бы исследователь затруднялся описать некую модельную связь строго однозначно и воспользовался бы для формализации своего представления об объекте исследования нефункциональным аппаратом (например, схемой из арсенала нечеткой логики). В дальнейшем мы, упрощая задачу настоящей статьи, не будем касаться вопросов построения нефункциональной модели. Возможно, мы посвятим этому предмету специальную работу.

Если мы рассматриваем экзогенные параметры как точно измеряемые или оцениваемые величины, то такую модель можно назвать детерминированной или четкой. Но эта модель вне учета наличной информационной неопределенности не выдерживает проверки на корректность. Поэтому, когда четкая функциональная модель дополняется вероятностным описанием экзогенных параметров, то такую модель следует назвать вероятностной. Если же описание экзогенных параметров модели носит нечетко-множественный характер, то такую модель назовем нечеткой.

Раз модель, описываемая нами, является функциональной, то неопределеннность в отношении экзогенных параметров (назовем ее Е1) трансформируется в неопределенность относительно уровня целевых параметров (назовем ее Е2), причем если существует конструктивное описание неопределенности Е1, то конструктивное описание неопределенности Е2 может быть построено вполне точно. Так, например, если экзогенные параметры представляются в модели как случайные величины со своими законами распределения, то целевые параметры являются функциями случайных экзогенных параметров, а вероятностные распределения целевых параметров строятся на основе распределений экзогенных параметров при помощи импликативных вероятностных схем.

Пример 1. Пусть в нашей модели Х — экзогенный параметр с плотностью вероятностного распределения f_X (x), а Y — целевой параметр, который функционально связан с Х как Y = X². Тогда плотность распределения целевого параметра Y, согласно теории функций случайных величин, имеет вид:

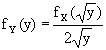(1)

Рассмотрим теперь, как учитывается неопределенность в маркетинговой модели с применением теории нечетких множеств.

Треугольные нечеткие числа, нечеткие последовательности и нечеткие функции

В настоящей публикации мы не имеем возможности дать развернутое изложение основ теории нечетких множеств. Однако, поскольку этот раздел математики еще не получил широкого распространения в экономических исследованиях, мы считаем своим долгом описать применяемые здесь математические объекты, относящиеся к этой теории.

Если некоторые экзогенные параметры маркетинговой модели обладают «размытостью», т.е. их точное планируемое значение неизвестно, тогда в качестве исходных данных уместно использовать так называемые треугольные нечеткие числа с функцией принадлежности треугольной формы (рис. 1). Эти числа моделируют высказывание следующего вида: «параметр А приблизительно равен и однозначно находится в диапазоне [a_min, a_max]». Основные понятия теории нечетких множеств см. в [3].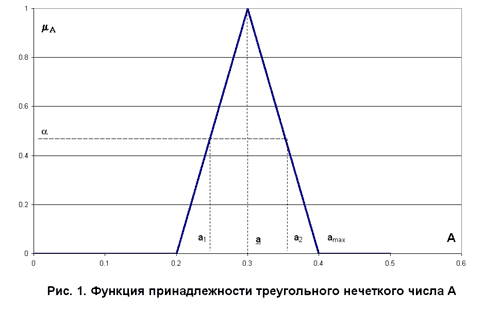

В общем случае под нечетким числом понимается нечеткое подмножество универсального множества действительных чисел, имеющее нормальную и выпуклую функцию принадлежности [3]. Такое описание позволяет разработчику маркетинговой модели взять в качестве исходной информации интервал параметра [a_min, a_max] и наиболее ожидаемое значение , и тогда соответствующее треугольное нечеткое число 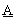= (a_min, , a_max) построено. Далее будем называть параметры (a_min, , a_max) значимыми точками числа .

Тогда нечеткая последовательность— это просто набор нечетких чисел со своими функциями принадлежности, где каждому нечеткому числу взаимно однозначно соответствует порядковый номер, принадлежащий множеству целых положительных чисел. Если заместить в этом определении набор действительных чисел на несчетное множество точек оси действительных чисел (область определения), а набор нечетких чисел — на несчетное множество нечетких чисел (область значений), то легко перейти к определению нечеткой функции как взаимно-однозначному соответствию оси действительных чисел и несчетного множества нечетких чисел. Если все нечеткие числа из упомянутой области значений нечеткой функции являются треугольными, то существует конструктивный способ задания этй нечеткой функции тремя обычными функциями, построенными на значимых точках соответствующих функций принадлежности: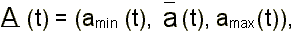
(2)

и тогда удобно называть соответствующую нечеткую функцию также треугольной.

На графике рис. 2 представлены три функции вида (2), отвечающие некоторой треугольной нечеткой функции. Область «размытости» представленной нечеткой функции продаж отмечена штриховкой.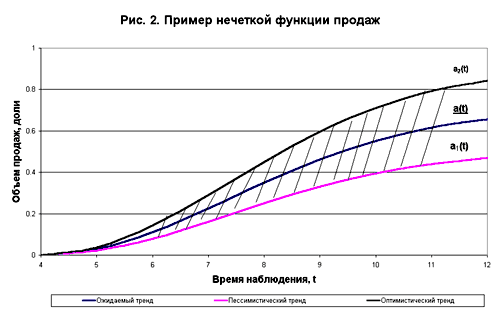


Теперь, когда необходимые нам определения введены, изложим подход к трансформации исходной строго детерминированной модели в модель, построенную на нечеткостях.

Метод замещения четкой модели нечеткой моделью

Пусть некоторый целевой параметр в результате моделирования приобретает вид функции

A (t) = A (t | а₁, m₁; а₂, m₂;…; а_N, m_N), (3)

где t — модельное время, А = (а₁, а₂, …а_N) — вектор экзогенных параметров, известных не вполне точно, M = (m₁, m₂,…, m_N) — набор индикаторов монотонности, когда выполняется

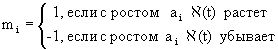(4)

Формула (3) представляет собой одно из описаний четкой модели. Дополнением к этой модели является нечеткое описание экзогенных параметров вектора А. Если мы их задаем треугольными нечеткими числами, тогда функция A (t) тоже является нечеткой. Будет ли она треугольной — это отдельный вопрос.

Чтобы получить конструктивное описание нечеткой функции при известных нечетких описаниях экзогенных параметров, применим сегментный способ, как это сделано в [2, 3]. Суть метода, применительно к двупараметрической задаче, состоит в следующем.

Зафиксируем значение модельного времени t₀ и исследуем описание нечеткого числа A (t₀) как функции двух нечетких параметров: и 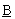. Зададимся фиксированным уровнем принадлежности a (см. рис. 1) и определим соответствующие этому уровню интервалы достоверности по двум нечетким числам и 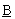: [a₁, a₂] и [b₁, b₂], соответственно. Тогда алгебраические операции с нечеткими числами сводятся к операциям с их интервалами достоверности. А операции с интервалами, в свою очередь, выражаются через операции с действительными числами — границами интервалов по следующим аксиоматическим правилам:

— операция «сложения»: [a₁, a₂] (+) [b₁, b₂] = [a₁ + b₁, a₂ + b₂], (5)

— операция «вычитания»: [a₁, a₂] (-) [b₁, b₂] = [a₁— b₂, a₂— b₁], (6)

— операция «умножения»: [a₁, a₂] (x) [b₁, b₂] = [a₁ x b₁, a₂ x b₂], (7)

— операция «деления»: [a₁, a₂] (/) [b₁, b₂] = [a₁ / b₂, a₂ / b₁], (8)

— операция «возведения в степень»: [a₁, a₂] (^) i = [a₁ⁱ, a₂ⁱ]. (9)

Пример 2. Пусть A (t₀ | А, m₁ =1; В, m₂ =1) = (А² + В²)^1/2 — нечеткая функция, где А = (2, 3, 4), В = (1, 2, 3) — треугольные нечеткие числа. Определим вид функции принадлежности нечеткой функции A в точке t₀. При фиксированном уровне принадлежности a соответствующий интервал достоверности [A ₁, A ₂] для нечеткого числа A (t₀) определяется в соответствии с (6) и (9) так:

[A ₁, A ₂] = ([a₁², a₂²] (+) [b₁², b₂²]) (^) (1/2) = [(a₁² + b₁²)^1/2, (a₂²+ b₂²)^1/2] (10)

В таблице 1 приведены интервалы достоверности для различных уровней принадлежности a в диапазоне от 0 до 1 с шагом 0.1.

Таблица 1

a	[a1, a2]	[b1, b2]	[A 1, A 2]
0.0	[2, 4]	[1, 3]	[2.24, 5]
0.1	[2.1, 3.9]	[1.1, 2.9]	[2.37, 4.86]
0.2	[2.2, 3.8]	[1.2, 2.8]	[2.51, 4.72]
0.3	[2.3, 3.7]	[1.3, 2.7]	[2.64, 4.58]
0.4	[2.4, 3.6]	[1.4, 2.6]	[2.78, 4.44]
0.5	[2.5, 3.5]	[1.5, 2.5]	[2.92, 4.30]
0.6	[2.6, 3.4]	[1.6, 2.4]	[3.05, 4.16]
0.7	[2.7, 3.3]	[1.7, 2.3]	[3.19, 4.02]
0.8	[2.8, 3.2]	[1.8, 2.2]	[3.33, 3.88]
0.9	[2.9, 3.1]	[1.9, 2.1]	[3.47, 3.74]
1.0	[3, 3]	[2, 2]	[3.61, 3.61]

В самом общем случае функция треугольных чисел не есть треугольное число. Однако для большого разнообразия функций (как и для примера 2) функция принадлежности нечеткого числа A может быть приведена к треугольному виду, а сама нечеткая функция — признана треугольной.

Таким образом, мы получаем нечеткую функцию целевого параметра, приведенную к треугольному виду (например, объем продаж). В финансовом плане инвестиционного проекта этот параметр выступает уже как экзогенный, причем, поскольку в бизнес-плане бюджетирование проводится в дискретном времени, то вместо нечеткой функции финансовый план может использовать нечеткую последовательность объемов продаж, например, с поквартальной разбивкой. По аналогии с функциональной маркетинговой моделью мы заметим, что тогда точечные показатели эффективности инвестиционного проекта (скажем, чистая современная ценность проекта) являются треугольными нечеткими числами. Следовательно, можно решить задачу оценки риска инвестиций в подобный проект, как это сделано в [2].

Пример 3. Модель роста продаж продукции ЗАО «ABC»

Попробуем обобщить все изложенное на примере. Для ясности мы будем рассматривать конкретный проект, связанный с выводом на рынок новой марки потебительского товара — водки. Эта задача имеет свой предметный аналог, и ее результат может быть применим, например, для оценки эффективности инвестиционного проекта по созданию нового ликеро-водочного производства.

Рассмотрим ситуацию, сложившуюся с продажей алкогольных напитков в N-ском районе одной из областей Северо-Западного региона России. В силу отдаленности этого района от крупных производителей вино-водочной продукции эта продукция представлена на рынке N-ского района всего двумя секторами:

сектором продаж водки, производимой на местном ЗАО «АВС» (назовем этот сектор сектором АВС);

сектором продаж водки, производимой конкурентом ЗАО «АВС» — иногородней фирмой «Х». Назовем этот сектор сектором Х.

ЗАО «АВС» является новым предприятием, только что приступившим к выпуску алкогольной продукции. Однако оно имеет серьезные конкурентные преимущества перед фирмой Х, поскольку не несет глобальных транспортных затрат на ввоз водки в регион. Также ЗАО «АВС» может в ходе рекламной компании акцентировать свою «местную» принадлежность, призывая потребителя сделать выбор в пользу «своего», что даст региону дополнительные налоговые поступления и рабочие места. Такая сильная «патриотическая» имиджевая позиция, вкупе с облегченной структурой затрат, позволяет сделать вывод о том, что новая «местная» марка водки со временем серьезно потеснит продукцию сегмента Х. Остается оценить, какими темпами будет производиться это вытеснение.

Метод решения на основе четкой модели

Если мы зададимся наиболее ожидаемыми значениями экзогенных параметров, то будем решать нашу задачу в рамках четкой модели. Затем, размыв исходные параметры, мы перейдем к нечеткому описанию функции продаж.

Обозначим объем продаж в секторе АВС за L(t), млн л. в месяц, где t — номер месяца с момента начала наблюдения за рынком (начало продаж ЗАО «ABC»). Также обозначим объем продаж в секторе Х за K(t), млн. литров в месяц.

Тогда выполняется равенство

L(t) + K(t) = F(t) = F_max x d (t), (11)

где F(t) — суммарный объем продаж водки, F_max— предельное ожидаемое значение продаж в календарном году, d (t) — функция сезонности спроса. Согласно проведенным расчетам, предел продаж F_max— в обеих секторах рынка водки в N — ском районе составляет 3 млн. литров в месяц.

Сделаем допущения о функции сезонности спроса d (t). Она является периодической функцией с периодом один календарный год и принимает одни и те же значения по всему Северо-Западу России. Маркетологические исследования, ранее проведенные специалистами, дают табличный вид этой функции (см. табл. 2), если за t обозначить номер календарного месяца по порядку их следования (в общем случае номера t и t не совпадают):

Таблица 2

t	Название месяца	Значение d t	t	Название месяца	Значение d t
1	Январь	d 1 » 0.92	7	Июль	d 7 » 0.50
2	Февраль	d 2 » 0.85	8	Август	d 8 » 0.58
3	Март	d 3 » 1.00	9	Сентябрь	d 9 » 0.65
4	Апрель	d 4 » 0.77	10	Октябрь	d 10 » 0.65
5	Май	d 5 » 0.62	11	Ноябрь	d 11 » 0.73
6	Июнь	d 6 » 0.54	12	Декабрь	d 12 » 0.85

То есть, справедлива формула:

(12)

Для того, чтобы перейти к моделированию кривой продаж по ЗАО «ABC», необходимо перейти от сезонной зависимости продаж к внесезонной, учитывающей только перераспределение долей продаж между ЗАО и конкурентами. Разделим обе части равенства (11) на F(t). Тогда

j (t) + y (t) = 1, (13)

где j (t) = L(t) / F(t) — удельный объем (доля) продаж ЗАО «ABC», y (t) = K(t) / F(t) — то же для конкурентов. Качественный вид функций j и y см. рис. 3.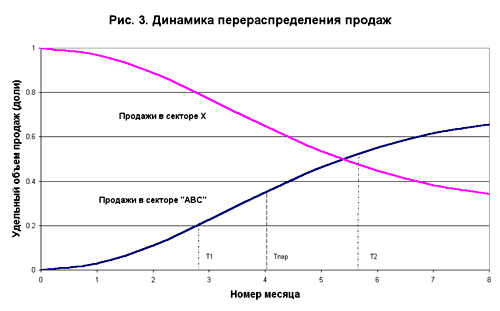

Поскольку функции j и y линейно зависимы, то в последующем мы будем рассматривать только динамику по ЗАО «ABC». Выдвинем основные допущения к качественному виду функции j :

1. Ясно, что по прошествии времени ЗАО «ABC» не останется единственным продавцом на рынке N-ского района, а достигнет некоего максимума продаж в долевом отношении. Как уже оговаривалось, мы не будем заниматься теоретическим вычислением вероятного значения этого макимума, и удовольствуветмся принятием целевого значения, определенного экспертным путем. Обозначим этот максимум j _max. В нашей задаче методом экспертных оценок определено наиболее ожидаемое значение j _max = 0.7.

Тогда мы можем строить модель j (t) в виде

j (t) = j _max x R(t, r, b), (14)

где R(t, r, b) — профильная кривая, принимающая значения от 0 до 1, r — параметр формы, b — параметр масштаба.

2. Профильная кривая условно может быть сегментирована по оси абсцисс на три интервала:

а) интервал [0, Т1], соответствующий фазе начала продаж. Торговая марка еще неизвестна потребителю, однако она активно рекламируется. ЗАО вкладывает средства в развитие своей дилерской сети, проводит специализированные маркетинговые мероприятия по популяризации новой торговой марки (презентации, специальные праздничные скидки и проч.). Формируется элемент привыкания потребителя к новому продукту;

б) интервал [Т1, Т2], соответствующий фазе квазилинейного роста продаж. На этом этапе начинают окупаться усилия, вложенные в рекламную компанию. Торговая марка водки и ее производителя достигает возможного максимума «раскрученности», этот максимум соответствует точке перегиба профильной кривой R. Потребитель положительно оценил новый напиток и включил его в свой продуктовый набор, вытеснив из своего потребительского портфеля продукцию конкурентов;

в) интервал [Т2, inf], соответствующий фазе насыщения. В основном сформировался контингент, выбравший напиток новой марки для регулярного потребления. Приращение рекламного бюджета уже не приводит к адекватному росту рыночной доли. Если качество напитка со временем не меняется, то происходят лишь незначительные колебания спроса в сторону снижения или повышения, взаимно компенсирующие друг друга. Бесконечность в качестве верхней границы интервала выбрана условно. На самом деле, время наблюдения ограничено сроком жизни наблюдаемой торговой марки.

3. Таким образом, профильная кривая R характеризуется следующими количественными и качественными особенностями:

а) при t = 0 R = 0;

б) при t = inf R = 1;

в) кривая R имеет точку перегиба (в этой точке вторая производная кривой R равна нулю).

Если бы новый товар не встречал сопротивления конкурентов в своем продвижении на рынок, тогда следовало бы искать функцию R в экспоненциальной или показательной форме, как это делается, например, в [1]. Но сопротивление вызывает перегиб функции, и ее приходится искать в двупараметрической форме. Одним из лучших приближений профильной кривой R, с учетом выдвинутых к ней требований, является кривая Вейбулла:

R(t, r, b) = 1 — exp (- (t / b)^r) (15)

с параметром формы r = 2 (такое значение параметра r обеспечивает кривой R приемлемую гладкость). Чем больше значение b, тем медленнее будут нарастать продажи ЗАО.

Чтобы определить значение параметра b, необходимо задаться координатой одной из характерных точек на кривой R. В качестве такой точки может служить момент времени, когда новая торговая марка займет порядка 50% от своего предельного долевого уровня на региональном рынке (R = 0.5, j (Т_пер) = j _max /2 = 0.35). Этому значению соответствует момент Т_пер, который определяется по нетрудно выводимой на основе (15) формуле при r = 2:

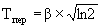, (16)

откуда получаем значение b :

. (17)

Опять же методом экспертного опроса был определен параметр Т_пер, и его наиболее ожидаемое значение составило 4 месяца.

В итоге, результирующее оценочное значение уровня продаж ЗАО «ABC» во времени, с учетом всего изложенного, составляет:

L(t) = F_max x d (t) x j _max x (1 — exp (- (t / b)^r), (18)

где d (t) определяется (12) и таблицей 2, r = 2, а b вычисляется по (17) и составляет 4.8 месяца.

Пусть предприятие «АВС» начинает продажи в апреле 2000 года, т.е. смещение между номерами календарных месяцев t и номерами месяцев наблюдения составляет 4. Проведем расчеты по формулам (12) — (18). Результаты расчетов сведены в таблицу 3.

Таблица 3

t	d (t)	R(t, r, b)	L(t), млн. л в месяц
0	0.77	0.000	0.00
1	0.62	0.042	0.06
2	0.54	0.159	0.18
3	0.50	0.323	0.34
4	0.58	0.501	0.61
5	0.65	0.662	0.90
6	0.65	0.790	1.08
7	0.73	0.881	1.35
8	0.85	0.938	1.67

Таким образом, целью специальных маркетинговых исследований по рынку водки в N-ском районе может быть определение следующих трех экзогенных параметров модели продаж:

1. F_max— предельный размер рынка водок данного класса в N-ском районе, млн. л в месяц.

2. j _max— предельно достигаемая доля ЗАО «ABC» на рынке водок данного класса,%.

3. Т_пер— срок, за который торговая марка ЗАО «ABC» займет 50% от своего предельного уровня на региональном рынке, месяцев.

Также в качестве экзогенного параметра модели выступает вектор сезонности спроса d (t). А целевым параметором модели является натуральный объем продаж водки «АВС», причем в качестве самой модели выступает функциональное соотношение (18).

Теперь, чтобы адекватно учесть фактор приближенности экспертных оценок, осуществим замещение четкой модели нечеткой, с заменой точных значений экзогенных параметров нечеткими числами.

Трансформация решения задачи с помощью нечетких функций

Мы не можем совершенно конструктивно оценить степень точности, с которой эксперты достигают своих количественных оценок рынка. Однако мы можем задаться расчетным параметром l степени «размытия», степени нечеткости модели. Чем больше l, тем шире расчетный диапазон экзогенных параметров, тем шире и расчетный диапазон нечеткой функции целевого параметра модели. Когда модель будет построена до конца, т.е. до оценки риска инвестиций, исследователь может оценить степень риска инвестиционного решения в зависимости от степени нечеткости исходных данных — и тем самым проанализировать устойчивость принимаемого решения к исходной информационной неопределенности.

Итак, замещаем в модели точные экзогенные параметры вектора А на треугольные нечеткие числа вида (А x (1 — l), А, А x (1 + l)). Пусть, для примера, степень нечеткости модели составляет 20%. Тогда расчет минимальных, ожидаемых и максимальных значений функции L(t) сведен в таблицу 4.

Таблица 4

t	d (t)			R(t, r, b)			L(t), млн. л в месяц
	мин	ожид	макс	мин	ожид	макс	мин	ожид	макс
0	0.62	0.77	0.92	0.00	0.00	0.00	0.00	0.00	0.00
1	0.50	0.62	0.74	0.03	0.04	0.07	0.04	0.06	0.08
2	0.43	0.54	0.65	0.11	0.16	0.24	0.12	0.18	0.26
3	0.40	0.50	0.60	0.24	0.32	0.46	0.22	0.34	0.49
4	0.46	0.58	0.70	0.38	0.50	0.66	0.39	0.61	0.88
5	0.52	0.65	0.78	0.53	0.66	0.82	0.58	0.90	1.30
6	0.52	0.65	0.78	0.66	0.79	0.91	0.69	1.08	1.55
7	0.58	0.73	0.88	0.77	0.88	0.96	0.86	1.35	1.94
8	0.68	0.85	1.02	0.86	0.94	0.99	1.07	1.67	2.41

Если мы договорились привести функцию L(t) к треугольному виду, то таблица 4 содержит конструктивное описание этой функции. Если договоренности о подобной аппроксимации нет, необходим требуемый уровень дискретизации оси времени и соответствующая экстраполяция параметров функций принадлежности в промежуточных точках.

Заключение

Без ложной скромности осмеливаемся заявить свое первенство в приложении математики нечетких множеств к задачам маркетингового моделирования. Здесь математика подобного рода, как и вообще в экономических задачах, оказывается как нельзя более кстати. Субъективные вероятности, прежде широко применяемые в экономическом анализе, сегодня встречают серьезные теоретические препятствия в использовании. В частности, подвергается сомнению безусловное применение критерия максимума энтропии Гиббса-Джейнса, лежащего в основе обоснования наиболее правдоподобных вероятностных распределений (подробнее об этом в [4]). Нечетко-множественный подход не сталкивается с затруднениями подобного рода. Он имеет дело не с возможностью, а с ожидаемостью. Он опирается на интуитивное знание исследователя рынка об ожидаемом диапазоне разброса экзогенных параметров. И если исходная неопределенность описана исследователем адекватно, в форме ожидаемых интервальных диапазонов, тогда оценка разброса целевых параметров модели, базирующася на применении обоснованных здесь нечетких функций и последовательностей, становится только делом техники.

© 1999 Алексей Недосекин, Антон Овсянко,
КГ «Воронов и Максимов»

Литература

1. Lilien G., Kotler Ph. Marketing Decision Making: A Model-Building Approach. N.Y.: Harper & Row Publishers, 1983.
2. Недосекин А.О. Применение теории нечетких множеств к задачам управления финансами // Аудит и финансовый анализ, 2000, № 2.
3. Кофман А., Хил Алуха Х. Введение теории нечетких множеств в управлении предприятиями. Минск, Вышэйшая школа, 1992.
4. Смоляк С.А. Учет специфики инвестиционных проектов при оценке их эффективности // Аудит и финансовый анализ, 1999, № 3.

Алексей Недосекин, Антон Овсянко
Консультационная группа «Воронов и Максимов»